Electronic voting systems were initiated early 2000s at the dawn of the Internet.
In the last 20 years, software designers have mobilized huge energy to secure their solution and attempt to prove that the system was reliable, without reaching absolute certainty.
Voting is a tool of democracy, for which trust in the system is decisive and corollary, doubt is a poison that provokes a lot of damages.
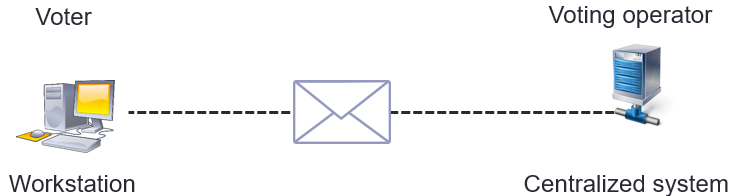
An unreliable architecture design
Designers of these systems defined a technical architecture based on the principles used at the time, a client-server architecture: a workstation communicating with a central computer through the network.
The internet works on the same principle as the private network was the working hypothesis.
The solution assumes that a secure tunnel is established between the two parties. However, we can notice the following facts:
- The network transits into the public domain. It is therefore exposed and hackable.
- The IP communication protocol establishes a link that is structurally discontinuous, it is deemed as unreliable.
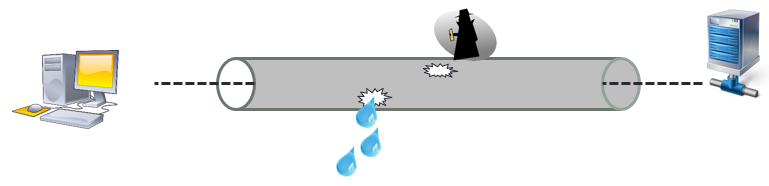
Therefore, a solution that assumes that the communication channel is secure will bring some disappointments.
A paradigmatic shift
We have to imagine a solution while using a potentially corrupt link. The main issue is to prove that the transmitted packet is identical on both sides of the link.

The data packet (the vote) is the unit to preserve. We have to prove to the stakeholders that the vote stored by the operator has not been changed or altered throughout the operation.
I named the architecture of the proposed solution « verifiability by hash symmetry » .
The solution is based on two cryptographic tools: encryption and hash function.
Definition: RSA encryption
Cryptography method that makes the comprehension of an encrypted document impossible for anyone who does not have the decryption key.
Algorithm of asymmetric cryptography
Uses a pair of keys composed:
– a public key to encrypt.
– a private key to decrypt confidential data.
Definition: Hash function SHA (Secure Hash Algorithm)
SHA is a cryptographic function that produces a digital hash.
– For a given hash value (the hash), it is impossible to reconstruct a block of data with this hash value.
– We can’t modify a data block without changing its hash value.
– We can’t find two different messages with the same hash value.
SHA-3 256
Function described in August 2015 by FIPS-202 publication
More robust than SHA-1 and SHA-2.
Description of a voting sequence.
a) Initialization of the voting operation
# 1 Ballot box initialization.
Encryption keys (asymmetric) creation.
The keys will encrypt the data packet (the vote, represented by the yellow tennis ball in the following diagrams) and not the database that stores all the votes.
#2 Creating an identity register as a hash list
The vote operator (usually a state) defines a set of data which he considers to be sufficient to authenticate a person. For example, in Geneva the voting card number (received by post mail), the date of birth and the municipality of origin are considered sufficient to authenticate a voter.
The voting operator build two lists:
- The register of names and voting card numbers
- The register of voting card number + date of birth + place of birth
The first list is used for printing voting cards and sending them to the voter.
The second list is intended to generate the ID (hash) of each voter. All hashes are then stored in an Identity Register (ID).
The second list used to generate the hash is destroyed after the hash operation. Thus, only the ID hash register remains. So, it’s impossible to recreate the identity of the voter based on his hash.
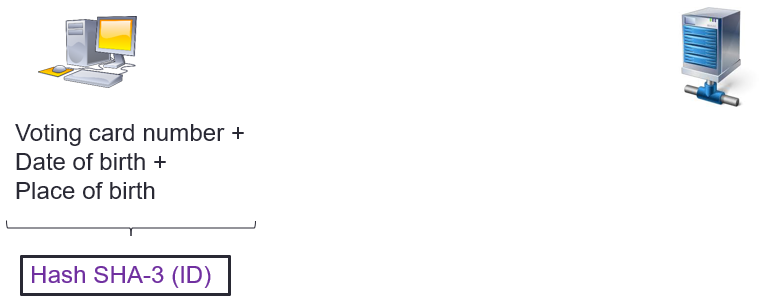
Thus, the system has created the identification of a person without making any connection with his identity. It is therefore not possible to reconstruct the identity of a person based on his ID hash.
b) Voting process
# 3 Download the software and the vote description
The voter downloads a package of tools that allows him to vote.

The package contains the following tools:
- The software: the presentation layer, the hash and encryption tools.
- The description: the subject of the vote and encryption key.
The presentation layer is used to build the interface and the voting software on the user side. The subject of the vote describes the list of objects or persons that constitute the ballot.
To ensure that the received tool package is the good one, the footprint of the downloaded package is calculated on the workstation. The resulting hash is compared with the hash ID contained in the operator’s server. They must be the same.
#4 Vote: ID calculation
The voter fills the webform with the needs data to authenticate it. Those data are hashed with the software downloaded it in the previous step. Then it generates its own identity SHA-3 (ID) hash.

#5 Vote: individual vote
The voting interface is generated based on the description of the voting objects received in the software toolkit described in sequence #3.
The vote is made by the voter.
The voting system build a voting package.
- Voting data + a random string (padding) are encrypted with the public key of the operation.
Then a SHA-3 (vote) hash is calculated for this element - The voting package includes: the encrypted voting data + the voter ID hash.
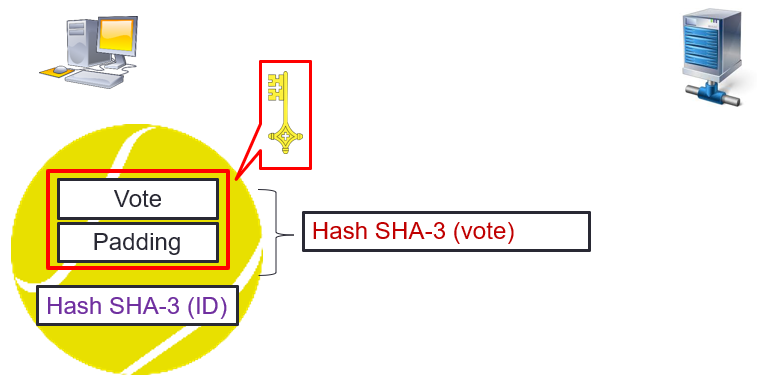
The voter store locally his voting hash and his identity hash (SHA-3 ID + SHA-3 vote).
The random string (padding) inserted into the voting string allows two even positions to not have the same hash. The hash is unique for each vote, which will be decisive for the proof (verifiability).
Thus, the voting package includes the encrypted vote as well as the hash of the voter ID.
The vote can only be decrypted using the private key of the voting operator. The hash of the voter’s ID is transmitted knowing that nobody is able to reconstruct his identity.
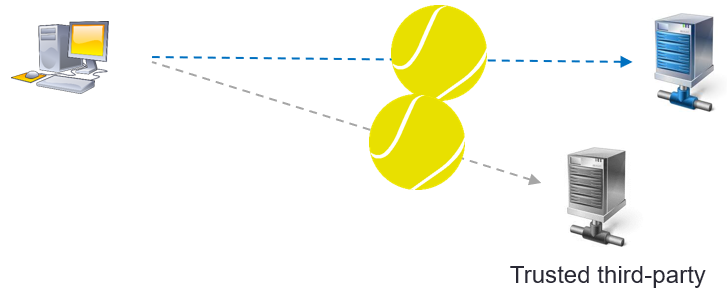
#6 Vote: send the vote
The voting package is sent to the server of the operator.
It is possible to set up a trusted third-party server.
In this case, vote packages will be systematically sent to both servers.
Thus, a third authority that received all votes will be able to carry out the operation for its own and to compare the result.
#7 Voting processing, ID
Upon receipt of the voting packet, the server will separate the ID hash and the encrypted vote.
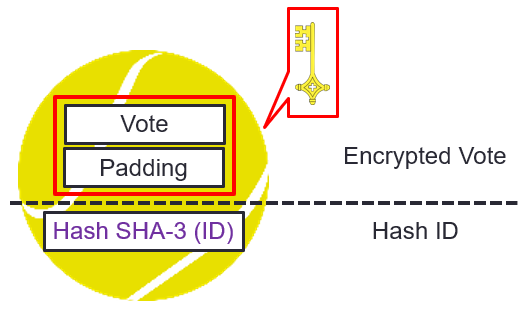
The server verifies the correspondence between the received ID hash with the identical hash contained in the ID hash register.
- If the ID is found, the ID in the registry ID is burned.
- If the ID is invalid, the vote is rejected and a notification is sent to the user for an invalid ID.

#8
Voting process, the vote
The vote received is encrypted, reading its content is
impossible.
- The central system computes the hash (vote) of the encrypted vote.
- The encrypted vote and his hash are stored on the central system.
- The hash calculated by the central server is returned to the voter.
The hash calculated by the voter’s computer is compared to the hash calculated by the server.
- If hashes are identical, the vote is accepted. The operation is complete.
- If hashes are different, an alarm is logged in the server and the vote is dismissed.
Voting is an atomic transaction.
c) Verifiability
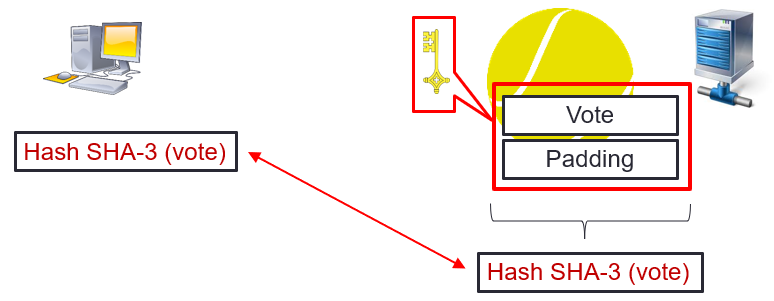
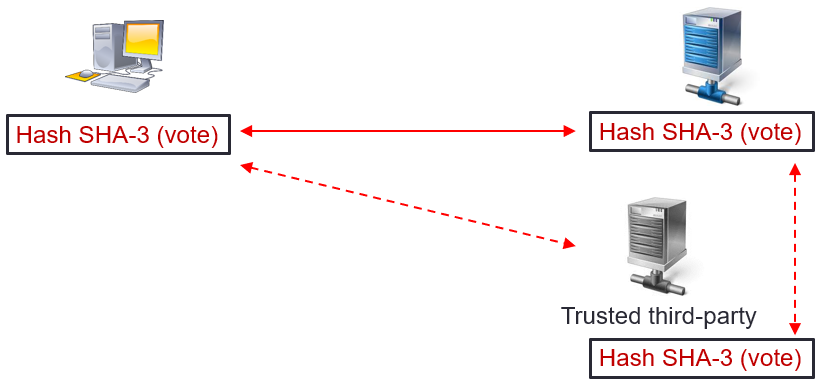
Before the count, the voter can at any time check that his vote exists on the server.
To do so, the voter sends the hash (vote) to the server. The server checks the existence of the hash (vote) in the database and confirms being depositary of this same hash.
Moreover, this control operation is systematically executed when sending the bulletin.
If the hash, which is unique, is strictly identical for the voter and the server, the voter has the confirmation that his vote is taken into account, which constitutes the verifiability of the vote.
This is the principle of « verifiability by hash symmetry » .
In addition, if a trusted third-party is established, the verifiability can be carried out with the independent third-party.
d) Opening the ballot box
When opening the ballot box, each individual vote is decrypted with the private key owned by the voting operation.
Votes are now available and the server can compute the result.
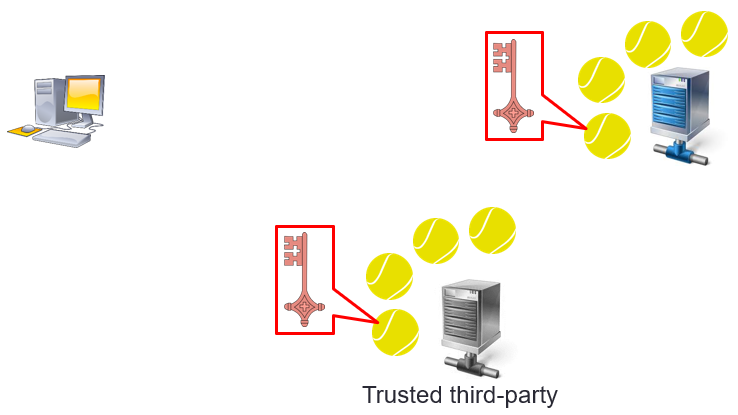
If a trusted third-party has been set up, the private decryption key is communicated to him by the operator during the opening of the ballot box.
The third-party has the votes and the decryption key. He can produce his own ballot count. This independent count strengthens trust in ballot counting.
Advantages of the system based on the verifiability by hash symmetry
The system has some advantages, among which:
- Simplified ergonomics for the user, no check table and multiple codes to deal with.
- Principles clear and understandable.
- Technically autonomous solution.
- Atomic transaction.
- Does not require encrypted transmission. However, a standard HTTPS transmission is settled for acknowledgments.
- Robust architecture.
- Strong against « man in the middle » hacking.
- Implicit verifiability.
- A trusted third-party can be integrated to the process.
Conclusions
This proposal has many advantages, but it certainly deserves to be debated in order to refine the approach, challenge security and validate the concept.
My only believe is that the solutions available on the market are technically obsolete and deficient from the point of view of security. They will have to be rethought with up to date technical solutions.
© Pascal Rulfi, September 2019. Any implementation of a system based on « verifiability by hash symmetry » contravenes intellectual property rights and / or copyright.
Download the document : e-voting

